物天学生发展中心期末力学复习讲义
往年试题
题型分布
与章末一致,为思考题加计算题形式。21年试卷为七道思考加三道计算,计算题有一道课本原题。重点考察章节为第四章与第六章,即刚体运动学与振动和波,总体来说难度不大。没有难题。
个人对力学的理解
基本就属于用微积分重写了一遍高中力学,做题的时候仍然需要把握住几个重要物理量,能量\(E\),动量\(\vec{p}\),以及在研究刚体时新引进的物理量角动量\(\vec{j}\)。还要习惯对矢量的微分积分运算。
各章重点概念,公式及定理
质点运动学
基本物理量
\(\vec{r}\)(位矢)、\(\vec{v}\)(速度)、\(\vec{a}\)(加速度)。 微分关系 \[ \begin{aligned} \vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\\ \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} \end{aligned} \] 积分关系 \[ \begin{aligned} \vec{r}=\int\vec{v}\mathrm{d}t\\ \vec{v}=\int\vec{a}\mathrm{d}t \end{aligned} \]
两种坐标系
平面直角坐标系
基向量为\(\vec{i}\)和\(\vec{j}\),且\(\vec{i}\)和\(\vec{j}\)为常矢量。在该坐标系中位矢,速度和加速度可以表示为 \[\begin{aligned} \vec{r}&=x\vec{i}+y\vec{j}\\ \vec{v}&=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\frac{\mathrm{d}x}{\mathrm{d}t}\vec{i}+\frac{\mathrm{d}y}{\mathrm{d}t}\vec{j}\\ \vec{a}&=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\frac{\mathrm{d}^2x}{\mathrm{d}t^2}\vec{i}+\frac{\mathrm{d}^2y}{\mathrm{d}t^2}\vec{j} \end{aligned} \]
极坐标
基向量为\(\hat{r},\hat{\theta}\),但是\(\hat{r},\hat{\theta}\)都是\(\theta\)的函数。即 \[
\begin{aligned}
\hat{r}=\hat{r}(\theta)\\
\hat{\theta}=\hat{\theta}(\theta)
\end{aligned}
\] 有重要关系 \[
\begin{aligned}
\mathrm{d}\hat{r}=\hat{\theta}\mathrm{d}\theta\\
\mathrm{d}\hat{\theta}=-\hat{r}\mathrm{d}\theta
\end{aligned}
\] 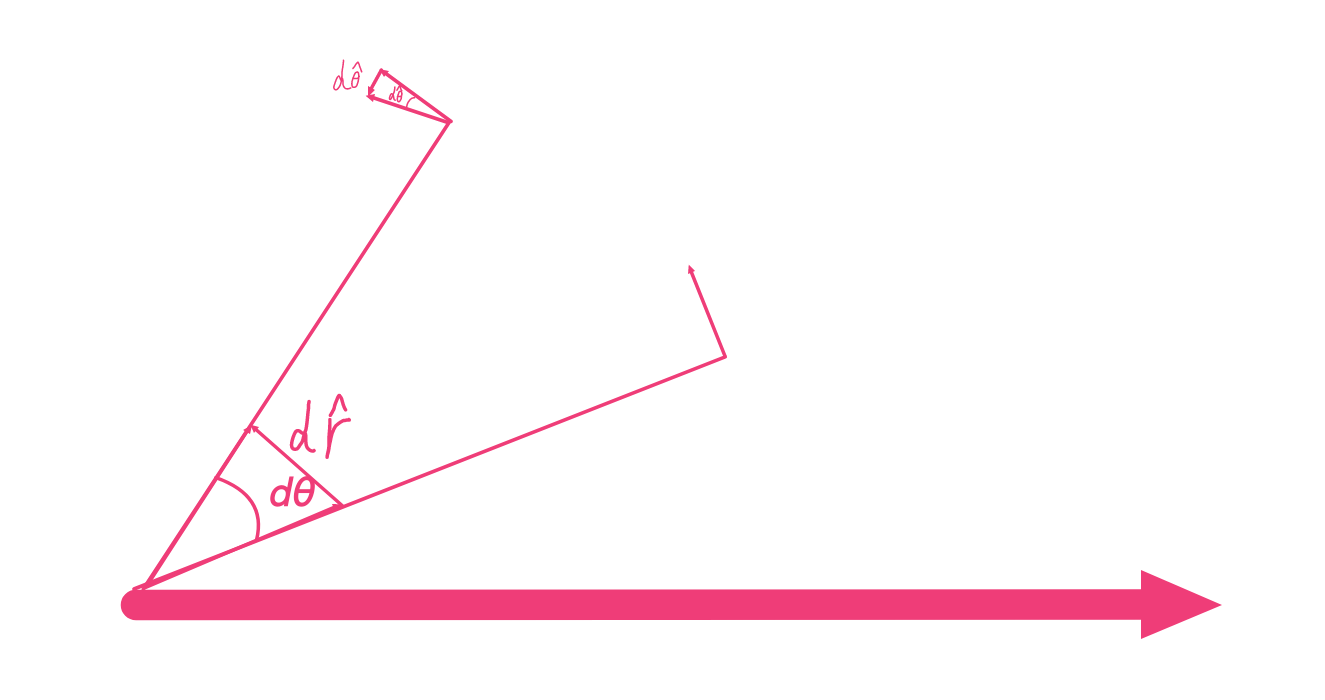 图中可以看到\(d\hat{\theta}\)与\(\hat{r}\)方向相反,\(d\hat{r}\)与\(\hat{\theta}\)方向相同。
故在极坐标中位矢,速度,加速度有如下表示 \[
\begin{aligned}
\vec{r}&=r\hat{r}\\
\vec{v}&=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\dot{r}\hat{r}+r\frac{\mathrm{d}\hat{r}}{\mathrm{d}t}=\dot{r}\hat{r}+r\dot{\theta}\hat{\theta}\\
\vec{a}&=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\ddot{r}\hat{r}+\dot{r}\frac{\mathrm{d}\hat{r}}{\mathrm{d}t}+\dot{r}\dot{\theta}\hat{\theta}+r\ddot{\theta}\hat{\theta}+r\dot{\theta}\frac{\mathrm{d}\hat{\theta}}{\mathrm{d}t}=(\ddot{r}-r\dot{\theta}^2)\hat{r}+(2\dot{r}\dot{\theta}+r\ddot{\theta})\hat{\theta}
\end{aligned}
\]
图中可以看到\(d\hat{\theta}\)与\(\hat{r}\)方向相反,\(d\hat{r}\)与\(\hat{\theta}\)方向相同。
故在极坐标中位矢,速度,加速度有如下表示 \[
\begin{aligned}
\vec{r}&=r\hat{r}\\
\vec{v}&=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\dot{r}\hat{r}+r\frac{\mathrm{d}\hat{r}}{\mathrm{d}t}=\dot{r}\hat{r}+r\dot{\theta}\hat{\theta}\\
\vec{a}&=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\ddot{r}\hat{r}+\dot{r}\frac{\mathrm{d}\hat{r}}{\mathrm{d}t}+\dot{r}\dot{\theta}\hat{\theta}+r\ddot{\theta}\hat{\theta}+r\dot{\theta}\frac{\mathrm{d}\hat{\theta}}{\mathrm{d}t}=(\ddot{r}-r\dot{\theta}^2)\hat{r}+(2\dot{r}\dot{\theta}+r\ddot{\theta})\hat{\theta}
\end{aligned}
\]
伽利略变换
\[ \left\{\begin{matrix} x'=x_0+X(t)\\ y'=y_0+Y(t)\\ z'=z_0+Z(t) \end{matrix}\right. \] \[ \begin{aligned} v'&=v_0+V(t)\\ V&=\dot{X}\vec{i}+\dot{Y}\vec{j}+\dot{Z}\vec{k}\\ a'&=a_0+A(t)\\ A&=\frac{dV}{dt} \end{aligned} \]
动量守恒,质点动力学
惯性系:对某一特定物体惯性定律成立的参考系。 物理定律在一切惯性系中相同。 \(m_惯\)是物体惯性大小的量度,\(m_引\)是物体产生引力大小的量度,这两者由等效原理确定相等。 动量\(\vec{p}=mv\)。动量既不会凭空产生也不会凭空消失。对于合外力为0的系统,其动量是守恒的。
火箭运动方程
设火箭行驶在重力可忽略的外层空间。以相对自身的恒定速率\(\vec{u}\)喷出燃料,求其运动方程。 系统动量守恒有 \[ \begin{aligned} m\vec{v}=(m-\mathrm{d}m)(\vec{v}+\mathrm{d}\vec{v})+\mathrm{d}m\cdot \vec{v}_{对地} \end{aligned} \] 由伽利略变换知 \[ \vec{v}_{对地}=\vec{u}+\vec{v} \] 故 \[ \begin{aligned} m\vec{v}=m\vec{v}+m\mathrm{d}\vec{v}-\mathrm{d}m\vec{v}-\mathrm{d}m\mathrm{d}\vec{v}+\mathrm{d}m\vec{u}+\mathrm{d}m\vec{v} \end{aligned} \] 略去二阶小量得 \[\begin{aligned} 0&=m\mathrm{d}\vec{v}+\mathrm{d}m\vec{u}\\ \mathrm{d}\vec{v}&=-\frac{\mathrm{d}m}{m}\vec{u}\\ \int_{0}^{v}\mathrm{d}\vec{v}&=-\vec{u}\int_{m}^{m_0}\frac{\mathrm{d}m}{m}\\ \vec{v}&=\vec{u}ln(\frac{m}{m_0}) \end{aligned} \] \(\ln(\frac{m}{m_0})<0\)代表\(\vec{v}\)和\(\vec{u}\)反向。
冲量定理
力是单位时间内物体在相互作用中传递的动量 \[ \vec{f}=\frac{\mathrm{d}\vec{p}}{\mathrm{d}t} \] 力的叠加原理:\(\frac{\mathrm{d}\vec{p_i}}{\mathrm{d}t}=\vec{f_i}=\sum_{i\neq j}f_{ij}\)
因为\(\vec{f}_{ij}=-\vec{f}_{ji}\)故\(\sum_{i\neq j}\vec{f_{ij}}=0\),即质点系内力矢量和为0,设\(\vec{P}=\sum_{i}\vec{p}_i\)则有质点系动量定理 \[ \frac{\mathrm{d}\vec{P}}{\mathrm{d}t}=\sum f_外 \] 力对时间的积累为冲量,记为\(\vec{I}\)。 \[ \vec{I}=\int\vec{f}\mathrm{d}t \] 动量定理表述为,外力冲量等于系统动量改变量 \[ \vec{I}=\int_{t_0}^{t_1}\vec{f}\mathrm{d}t=\vec{p}(t_1)-\vec{p}(t_0) \]
牛顿三定律
一、任何物体在不受力或受合外力为0时始终保持匀速直线运动或静止状态。(这个定律又被称为惯性定律,它定义了惯性系)
二、物体所受合外力等于物体动量变化率 \[
\vec{f}=\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}
\] 三、力的作用是相互的。
非惯性系与惯性力
定义一个惯性系\(K\)与一个非惯性系\(K'\)则惯性定律在\(K'\)中不成立,在\(K\)系中看起来静止或匀速直线运动的物体在\(K'\)系中并不是这样,它们的运动状态会发生改变看起来就像受力一样,我们把这种“看起来受的力”称为惯性力。在\(K'\)系相对于\(K\)系运动状态不同的情况下,惯性力也不同

机械能守恒
机械能=动能+势能
经典力学中动能是粒子速度的函数即\(T=\frac{1}{2}mv^2\),势能是粒子坐标的函数即\(V=V(\vec{r})\)。功的定义为\(\mathrm{d}A=F\cos(\theta)\mathrm{d}s\)。
势能场产生的力称为保守力,有如下关系 \[
\vec{F}=-\nabla V
\]
保守力沿任意闭合回路做功为0(保守力做功与路径无关)。保守系是所有非保守力都不做功的系统。
保守系中机械能守恒,即势能加动能为常量。
一维势能曲线
一维势能曲线告诉我们势能随坐标变化情况。即\(E_p-x\)图像, 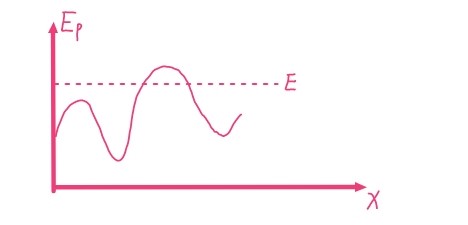 E为总能量,系统只能在虚线下面移动,虚线高度与系统系统纵坐标差值即为系统动能。
E为总能量,系统只能在虚线下面移动,虚线高度与系统系统纵坐标差值即为系统动能。
\(\frac{\mathrm{d}E_p}{\mathrm{d}x}=0\)的点我们称其为平衡点,极大值点为不稳平衡,极小值点为稳定平衡。
在极小值点周围的振动
若一质点初始静止在稳定平衡点,我们给其一个小扰动使其偏离平衡位置\(\Delta x\)的距离,则其机械能为 \[ E=T+U=0+U(x)=U(x_0+\Delta x) \] 对\(U(x)\)进行泰勒展开可得 \[ \begin{aligned} U(x_0+\Delta x)=U(x_0)+U'(x_0)\Delta x+\frac{U''(x_0)\Delta x^2}{2}+o(\Delta x^2) \end{aligned} \] 因为势能零点的选取是任意的,我们不妨将其选为\(x_0\),又因为\(U'(x_0)=0\),则质点势能可写为 \[ V(x)=\frac{U''(x_0)x^2}{2} \] 则其所受保守力为 \[ F=-\frac{\mathrm{d}\frac{U''(x_0)}{2}x^2}{\mathrm{d}x}=-U''(x_0)x \] 由牛顿第二定律得 \[ -U''(x_0)x=m\frac{\mathrm{d}^2x}{\mathrm{d}t^2} \] 这是一个简谐运动方程,\(\omega^2=\frac{U''(x_0)}{m}\),故其运动周期为\(T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{U^{''}(x_0)}}\)
质心与质心系
我们定义质点系的质心为 \[
\vec{r_c}=\frac{\sum_{i}m_i\vec{r}_i}{\sum_{i}m_i}
\]
关于质心,我们有一个很重要的推论,即质心系是一个零动量系,下面我们就来证明这条推论。
在实验室系中,系统总动量为 \[
\begin{aligned}
\vec{P}&=\sum m_i\vec{v}_i\\
&=\sum m_i\frac{\mathrm{d}\vec{r}_i}{\mathrm{d}t}\\
&=\sum
m_i\frac{\mathrm{d}(\vec{r}_c+\vec{r}_{ci})}{\mathrm{d}t}\\
&=\sum m_i\frac{\mathrm{d}\vec{r}_c}{\mathrm{d}t}+\sum
m_i\frac{\mathrm{d}\vec{r}_{ci}}{\mathrm{d}t}\\
&=\vec{v}_c\sum m_i+\sum
m_i\frac{\mathrm{d}}{\mathrm{d}t}(\vec{r}_i-\frac{\sum_{i}m_i\vec{r}_i}{\sum_{i}m_i})\\
&=\vec{v}_c\sum m_i+\frac{\mathrm{d}}{\mathrm{d}t}[\sum
m_i(\vec{r}_i-\frac{\sum_{i}m_i\vec{r}_i}{\sum_{i}m_i})]\\
&=\vec{v}_c\sum m_i+\frac{\mathrm{d}}{\mathrm{d}t}[\sum
m_i\vec{r}_i-\sum m_i(\frac{\sum_{i}m_i\vec{r}_i}{\sum_{i}m_i})]\\
&=\vec{v}_c\sum m_i+\frac{\mathrm{d}}{\mathrm{d}t}[\sum
m_i\vec{r}_i-\sum_{i}m_i\vec{r}_i]\\
&=\vec{v}_c\sum m_i
\end{aligned}
\] 在质心系中\(\vec{v}_c=0\),那么自然质心系就是一个零动量系了。
由上述推导我们还可以看出,质点系总动量就相当于所有质量都集中在质心上,并以质心速度运动,那么\(\frac{\mathrm{d}\vec{P}}{\mathrm{d}t}=\frac{\mathrm{d}\vec{v}_c}{\mathrm{d}t}\sum
m_i\)。又由动量定理知,\(\frac{\mathrm{d}\vec{P}}{\mathrm{d}t}=\vec{F}_外\),故
\[
\vec{F}_外=\frac{\mathrm{d}\vec{v}_c}{\mathrm{d}t}\sum m_i
\] 这就是质心运动定理。
柯尼希定理
系统总动能等于质心动能加质心系中动能,证明如下 \[\begin{aligned} E_k&=\sum\frac{1}{2}m_iv_i^2\\ &=\frac{1}{2}\sum m_i(\vec{v}_c+\vec{v}_{ic})^2\\ &=\frac{1}{2}\vec{v}_c^2\sum m_i+\vec{v}_c\sum m_i\vec{v}_{ic}+\frac{1}{2}\sum m_i\vec{v}_{ic}^2 \end{aligned} \] 由质心系动量定理的推导我们就已经知道\(\sum m_i\vec{v}_{ic}=0\),由此柯尼希定理得证。
两体问题
我们考虑特殊的系统仅由两个质点构成的问题,我们先引入相对速度的概念,即\(\vec{u}=\vec{v}_1-\vec{v}_2=\vec{v}_{1c}-\vec{v}_{2c}\),又因为在质心系中 \[ m_1\vec{v}_{1c}+m_2\vec{v}_{2c}=0 \] 故 \[ \begin{aligned} \vec{v}_{1c}&=\frac{m_2\vec{u}}{m_1+m_2}\\ \vec{v}_{2c}&=\frac{m_1\vec{u}}{m_1+m_2} \end{aligned} \] 则那么两体系统动能就为 \[\begin{aligned} E_k&=\frac{1}{2}(m_1+m_2)v_c^2+\frac{1}{2}m_1(\frac{m_2\vec{u}}{m_1+m_2})^2+\frac{1}{2}m_2(\frac{m_1\vec{u}}{m_1+m_2})^2\\ &=\frac{1}{2}(m_1+m_2)v_c^2+\frac{1}{2}\frac{m_1m_2}{m_1+m_2}u^2 \end{aligned} \] 我们就可以在质心系中将两体简化为质量为\(\frac{m_1m_2}{m_1+m_2}\),速度为\(\vec{u}\)的单个质点,即 \[ \begin{aligned} E_k=\frac{1}{2}(m_1+m_2)v_c^2+\frac{1}{2}\mu u^2 \end{aligned} \] \(\mu\)称为约化质量。在高能粒子实验中我们经常用一个粒子撞击另一个粒子,使其获得能量,碰撞过程便可看作一个两体问题,碰撞过程中只存在两粒子间的相互作用,故质心速度不变,即质心动能不变,真正能参与粒子间作用的能量就是我们刚刚得到的\(\frac{1}{2}\mu u^2\),这部分能量就称为资用能。
两体碰撞
两体碰撞是指在碰撞过程中仅存在两物体之间相互作用的问题,因为仅存在两物体之间相互作用,质心动量守恒。因此\(\vec{v}_c\)不变,在无能量损耗的情况下\(\vec{u}\)也不会改变,此时我们称其为弹性碰撞,有能量损耗的情况下,碰撞前后的相对速度并不相等,我们引进恢复系数\(e\)的概念,定义为 \[ e\equiv \frac{|u_1|}{|u_0|} \] \(e=1\)是弹性碰撞,\(e=0\)是完全非弹性碰撞,\(0<e<1\)是非弹性碰撞。
单位制与量纲
这个不是重点,主要用来对答案进行一个粗略的检查。
角动量守恒与刚体力学
我们首先引入角动量的概念,定义某质点对某点或某转轴的角动量时有 \[ \vec{j}=\vec{r}\times \vec{p} \] 对质点系而言,其对某点角动量等于各质点对质心角动量加上质心对给定点角动量 \[ \vec{j}=\sum\vec{r}_i\times \vec{p}_i=固有角动量\vec{J}_c+轨道角动量\sum \vec{r}_c\times \vec{v}_c \] 证明如下 \[ \begin{aligned} \vec{J}&=\sum m_i\vec{r}_i\times p_i\\ &=\sum m_i(\vec{r}_c+\vec{r}_{ci})\times (\vec{v}_c+\vec{v}_{ci})\\ &=m(\vec{r}_c\times \vec{v}_c)+\vec{r}_c\times \sum m_i\vec{v}_{ci}+(\sum m_i\vec{r}_i)\times \vec{v}_c+\sum \vec{r}_{ci}\times \vec{p}_{ci} \end{aligned} \] 质心系中\(\sum m_i\vec{v}_{ci}\)和\(\sum m_i\vec{r}_i\)均为0,故 \[ \vec{J}=m(\vec{r}_c\times \vec{v}_c)+\sum \vec{r}_{ci}\times \vec{p}_{ci} \]
力矩与角动量定理
外力矩等于系统角动量变化率 \[ \vec{M}=\sum\vec{r}_i\times \vec{F}_{i外}=\frac{\mathrm{d}\vec{J}}{\mathrm{d}t} \]
质心系角动量定理
质心系不一定是惯性系,但是质心系角动量定理与惯性系角动量定理具有相同的形式,证明如下 \[ \vec{M}_外=\sum\vec{r}_i\times \vec{F}_{i外}=\sum\vec{r}_{ci}\times \vec{F}_{i外}+\sum\vec{r}_c\times \vec{F}_{i外}=M_外'+\vec{r}_c\times \vec{F}_外 \] \[ \begin{aligned} \vec{J}&=\vec{J}'+m\vec{r}_c\times \vec{v}_c\\ \frac{\mathrm{d}\vec{J}}{\mathrm{d}t}&=\frac{\mathrm{d}\vec{J}'}{\mathrm{d}t}+m\frac{\mathrm{d}\vec{r}_c}{\mathrm{d}t}\times \vec{v}_c+m\vec{r}_c\times \frac{\mathrm{d} \vec{v}_c}{\mathrm{d}t}\\ &=\frac{\mathrm{d}\vec{J}'}{\mathrm{d}t}+\vec{r}_c\times m\frac{\mathrm{d} \vec{v}_c}{\mathrm{d}t} \end{aligned} \] \[\begin{aligned} \vec{M}_外&=\frac{\mathrm{d}\vec{J}}{\mathrm{d}t}\\ \frac{\mathrm{d}\vec{J}'}{\mathrm{d}t}+\vec{r}_c\times m\frac{\mathrm{d} \vec{v}_c}{\mathrm{d}t}&=\vec{M}_外'+\vec{r}_c\times \vec{F}_外\\ \frac{\mathrm{d}\vec{J}'}{\mathrm{d}t}&=\vec{M}_外' \end{aligned} \]
刚体动力学
刚体:形状和大小完全不变的物体
任意刚体的运动可分解为平动和转动。
平动:固连在刚体上的任何一条直线在各时刻的位置始终保持平行的运动。任一点的运动都可代表整体的平动,习惯上使用质心。
转动:刚体上所有点都绕同一直线(转轴)作圆周运动的运动。
角速度与角位移与转轴选取无关。
\[
\vec{\omega}=\frac{\overrightarrow {\mathrm{d}\theta}}{\mathrm{d}t}
\]
转动惯量
描述刚体绕某轴转动的惯性的大小,定义为 \[ I=\iiint_{V}\rho\vec{r}^2\mathrm{d}x\mathrm{d}y\mathrm{d}z \] 由定义可以得到两个非常有用的推论
平行轴定理
平行轴定理表述为,刚体对某轴转动惯量等于刚体质量乘以该轴距质心距离的平方加上刚体对平行于该轴且过质心的转轴的转动惯量。即 \[ I=I_c+mr^2 \] 证明: \[ \begin{aligned} I&=\iiint_{V}\rho(\vec{r}_c+\vec{r}_{oc})^2\mathrm{d}x\mathrm{d}y\mathrm{d}z\\ &=\rho\iiint_{V}\vec{r}_c^2\mathrm{d}x\mathrm{d}y\mathrm{d}z+2\iiint_{V}\vec{r}_c\rho\vec{r}_{oc}\mathrm{d}x\mathrm{d}y\mathrm{d}z+\rho\iiint_{V}\vec{r}_{oc}^2\mathrm{d}x\mathrm{d}y\mathrm{d}z\\ \end{aligned} \] 因为\(\iiint_{V}\rho\vec{r}_{oc}\mathrm{d}x\mathrm{d}y\mathrm{d}z=\iiint_{V}\vec{r}_{oc}\mathrm{d}m=0\),故 \[ I=m\vec{r}_c^2+\rho\iiint_{V}\vec{r}_{oc}^2\mathrm{d}x\mathrm{d}y\mathrm{d}z \] 得证
垂直轴定理
取直角坐标系,则绕三个坐标轴转动惯量为 \[
\begin{aligned}
I_z&=\iiint_{V}\rho(x^2+y^2)\mathrm{d}x\mathrm{d}y\mathrm{d}z\\
I_y&=\iiint_{V}\rho(z^2+x2)\mathrm{d}x\mathrm{d}y\mathrm{d}z\\
I_x&=\iiint_{V}\rho(z^2+y^2)\mathrm{d}x\mathrm{d}y\mathrm{d}z\\
\end{aligned}
\] 则有 \[
I_x+I_y+I_z=2\iiint_{V}\rho(x^2+y^2+z^2)\mathrm{d}x\mathrm{d}y\mathrm{d}z
\] 特别的对于薄板形物体有 \[
I_z=I_x+I_y
\] 该式不难证明,不再赘述。
下面给出几种常见均质几何体的的转动惯量表 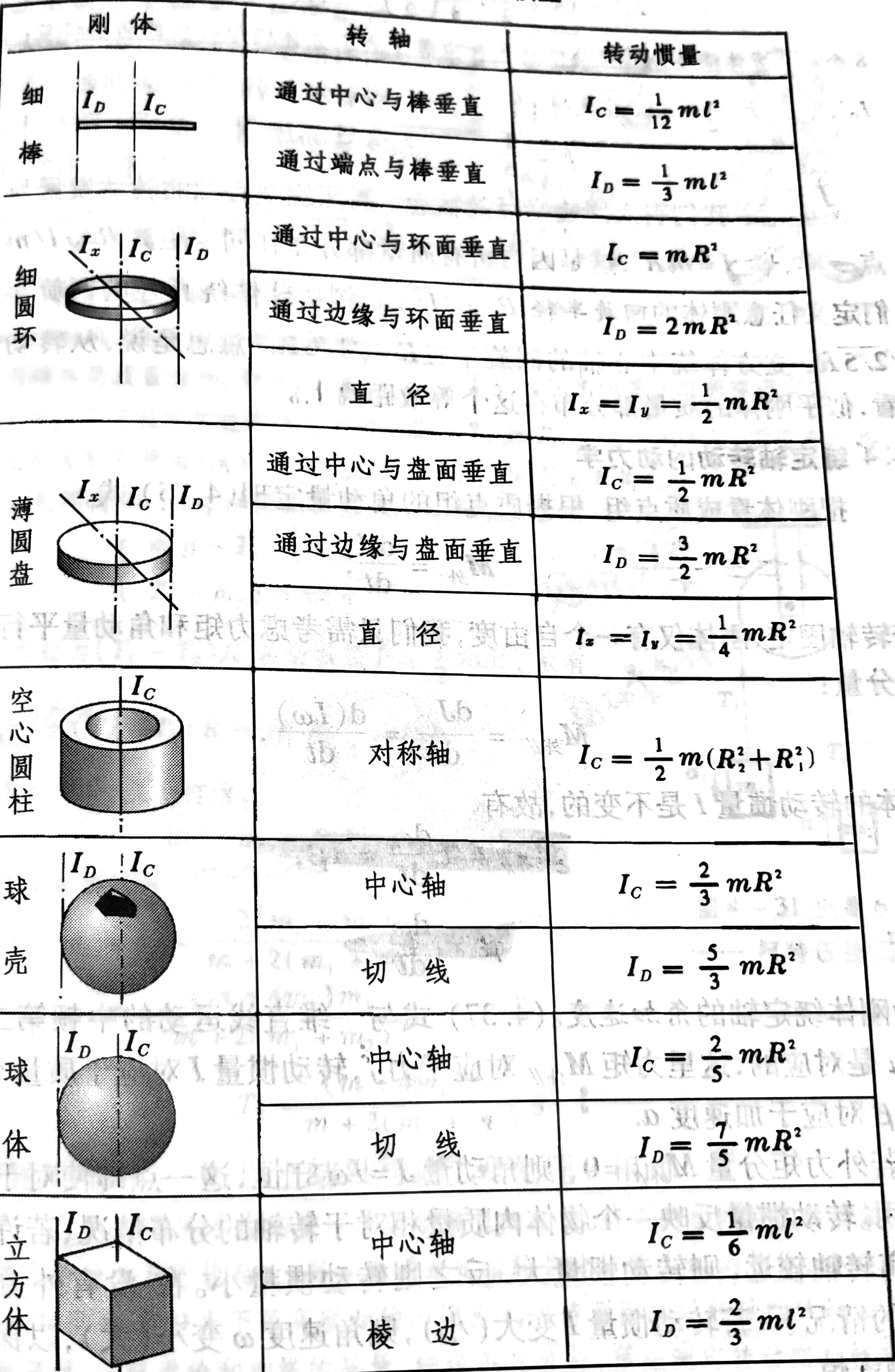 转动惯量类似于我们质点运动学中的质量。
转动惯量类似于我们质点运动学中的质量。
复摆周期
复摆力矩由重力提供,在小角近似下,力矩大小为\(mgr_c\theta\),运动方程为 \[ -mgr_c\theta=I\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2} \] 故复摆周期为\(T=2\pi\sqrt{\frac{I}{mgr_c}}\)
刚体平面平行运动
指的是所有质点运动平行于某一平面,动力学方程为 \[
\begin{aligned}
\vec{F}&=m\frac{\mathrm{d}\vec{v}_c}{\mathrm{d}t}\\
\vec{M}&=I\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}
\end{aligned}
\] 机械能为 \[
\begin{aligned}
E_p&=mgh\\
E_k&=\frac{1}{2}I_c\omega^2+\frac{1}{2}mv_c^2
\end{aligned}
\] 瞬心:刚体中瞬间速度为0的点。
纯滚动的限制条件就是接触点为瞬心。
刚体平衡条件
合外力为0,合外力矩为0
连续体力学
应力:连续体内部各部分之间单位面积的作用力。 \[
\mathrm{\tau}=\frac{\mathrm{d}\vec{f}}{\mathrm{d}S}
\] 固体中既有正应力\(\tau_\bot\)也有剪应力\(\tau_\parallel\)
静止流体只有正应力\(\tau_\bot\)
\(\tau_\bot=K \varepsilon_体\),\(\varepsilon_体=\frac{\Delta
V}{V}\)为体弹性模量
\(\tau_\parallel=G
\varepsilon_剪\),\(\varepsilon_剪=\theta\)为剪变角
对于直杆而言,两端应力为\(\frac{f}{S}\),则 \[
\tau=Y\varepsilon=Y\frac{\Delta l}{l_0}
\] 系数\(Y\)称为杨氏模量。
梁的弯曲
对于矩形截面梁,设其高为\(h\),宽为\(b\),则其曲率半径为\(\frac{Ybh^3}{12M_外}\)。
若截面为圆形,则曲率半径为\(\frac{\pi
Yd^3}{64M_外}\)。
再考虑竖直圆柱的稳定性,弯曲过程中增长的弹性势能为\(\int _0^\theta M_内\mathrm{d}\theta=\int _0^\theta
\frac{\pi Yd^4}{64R}\mathrm{d}\theta=\int _0^\theta \frac{\pi
Yd^4}{64l}\theta\mathrm{d}\theta=\frac{\pi
Yd^4}{128l}\theta^2\),减少的重力势能为\(-\frac{\pi d^2 l^2\rho
g}{192}\theta^2\),若减少的重力势能大于增长的弹性势能则立柱失稳,反之则稳定。
柱的扭转
研究方法为将圆柱切为半径不同的圆筒,这些圆筒产生的剪应力力矩应与外力矩平衡。计算可得 \[ M=\frac{\pi G R^4}{2l}\varphi=D\varphi \] \(D\equiv \frac{\pi G R^4}{2l}\)称为扭转常量,可见,力矩与扭转角成正比,由此性质,我们可以设置一个扭摆,那么运动方程就为 \[ I\frac{\mathrm{d}\varphi}{\mathrm{d}t^2}+D\varphi=0 \] 则周期为 \[ T=2\pi\sqrt{\frac{I}{D}} \]
表面张力
在两种不相溶液体或液体与气体之间会形成分界面,维持这层分界面的力称为表面张力 \[ \Delta f=\gamma \Delta l \] 空气中液滴能维持球形,也是依靠表面张力,液滴内外压差为 \[ \Delta p=\frac{2\gamma}{r} \] 毛细作用液柱高出液面也是依靠此压差维持。
理想流体定常流动问题
理想流体:不可压缩,无粘滞性。
定常流动:流场\(\vec{v}=\vec{v}(x,y,z)\),即流速不显含时间\(t\)。流场可用流线和流管来描述。 \[
流量\left\{\begin{matrix}
体积流量Q_V=\int\limits_{(S)}^{}\boldsymbol{v} \cdot
\mathrm{d}\boldsymbol{S} \\
质量流量Q_m=\int\limits_{(S)}^{}\rho \:\boldsymbol{v} \cdot
\mathrm{d}\boldsymbol{S}
\end{matrix}\right.\\
环量:\Gamma_C=\oint_{(C)}\boldsymbol{v}\cdot\mathrm{d}\boldsymbol{S}
\] 连续性原理:定常流动时,沿任意流管的横截面\(dS\)上 \[
\rho vdS 为常量
\]
伯努利方程
\[ \rho gh+\frac{1}{2}\rho v^2+p=常量 \] 条件:理想流体定常流动,同一流线。 实质:能量守恒定律。
粘滞流体
了解即可。
振动与波
简谐振动
所有运动方程形如 \[ \frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\omega^2x=0 \] 的运动都拥有相同形式的解 \[ x=A\cos(\omega t+\varphi) \] \(A\)和\(\varphi\)由初始条件给定。(二阶微分方程由两个常数确定解)
简正模
多自由度线性动力学系统的集体运动模式,每一模式有自己的运动频率(简正频率),相互独立,可以线性叠加。
阻尼振动
阻尼振动是指振子受一与运动速度成正比的阻力的运动,运动方程为 \[
\frac{\mathrm{d}^2s}{\mathrm{d}t^2}+\frac{\gamma}{m}\frac{\mathrm{d}s}{\mathrm{d}t}+\frac{k}{m}s=0
\] 令\(\frac{\gamma}{m}=2\beta\),\(\frac{k}{m}=\omega_0^2\),则方程变为 \[
\frac{\mathrm{d}^2s}{\mathrm{d}t^2}+2\beta\frac{\mathrm{d}s}{\mathrm{d}t}+\omega^2_0s=0
\] 该方程解的情况可分为三种情况
1、弱阻尼情况(\(\beta^2<\omega_0^2\))
方程解为 \[
s=Ae^{-\beta t}\cos(\sqrt{\omega_0^2-\beta^2}t+\varphi)
\] 即仍有振动,不过振幅随时间呈指数衰减。
2、临界阻尼情况(\(\beta^2=\omega_0^2\))
方程解为 \[
s=(A_1+A_2t)e^{-\beta t}
\] 此时质点回到平衡位置时间最短,不过没有振动。
3、过阻尼情况(\(\beta^2>\omega_0^2\))
方程解为 \[
s=A_1e^{-(\beta+\sqrt{\beta^2-\omega_0^2}t)}+A_2e^{-(\beta-\sqrt{\beta^2-\omega_0^2}t)}
\] 此时没有振动。
受迫振动
即质点还受到外界驱动力,我们只研究\(\boldsymbol{f}=\boldsymbol{F}\cos(\omega
t)\)的情况,运动方程变为 \[
\frac{\mathrm{d}^2s}{\mathrm{d}t^2}+2\beta\frac{\mathrm{d}s}{\mathrm{d}t}+\omega^2_0s=F\cos(\omega
t)
\] 不妨设解具有$s=e^{t} $的形式。
方程变为 \[
\tilde{A}e^{\mathrm{i}\omega t}(-\omega^2+2\beta
\mathrm{i}\omega+\omega_0^2)=\frac{F}{m}e^{\mathrm{i}\omega t}
\] 解得 \[
\tilde{A}=\frac{F}{m(-\omega^2+2\beta \mathrm{i}\omega+\omega_0^2)}\\
s=\tilde{A}e^{\mathrm{i}\omega t}\\
v=\mathrm{i}\omega\tilde{A}e^{\mathrm{i}\omega t}
\]
简谐波
\(u(x,t)=A\cos[2\pi(\frac{t}{T}\mp
\frac{x}{\lambda})+\varphi_0]=A\cos(\omega t\mp
kx+\varphi_0)\),复数\(\tilde{u}=\tilde{A}e^{\mathrm{i}(\omega t\mp
kx)}\)是空间位置和时间的函数。取正号时向\(-x\)方向传播,取负号时向\(-x\)方向传播。
相速度:\(c=\frac{\lambda}{T}=\frac{\omega}{k}\)相位传播速度
色散关系:\(\omega=\omega(k)\)或\(c=c(k)\)
群速:\(v_\mathrm{g}=\frac{\mathrm{d}\omega}{\mathrm{d}k}\)能量传播速度
一维弹性波
无穷长弹簧振子链为模型,\(\kappa\)是弹簧劲度系数,\(m\)是振子质量,\(a\)是振子间隔,\(\omega_0=\sqrt{\frac{\kappa}{m}}\)是固有频率,\(k\)是角波数。
运动方程为 \[
m\frac{\mathrm{d}^2u_n}{\mathrm{d}t^2}=\kappa(u_{n+1}-u_{n})-\kappa(u_{n}-u_{n-1})
\] 可取向右传播解 解得\(\omega=2\omega_0\sin(\frac{ka}{2})\),若波长远长于传播介质晶格长度,即\(\lambda\gg a\),则\(\omega=\omega_0ka\),\(c=\frac{\omega}{2\pi}\lambda=\omega_0a\),即波速与波长无关。
群速:\(v_\mathrm{g}=\frac{\mathrm{d}\omega}{\mathrm{d}k}=\omega_0a\cos\frac{ka}{2}\overset{长波极限}{\rightarrow}
\omega_0a\)
能量密度:\(\varepsilon=\frac{m}{2a}\omega^2A^2\overset{长波极限}{\rightarrow}\frac{\kappa
ak^2}{2}A^2\)
能流密度:\(\varpi=\frac{\sqrt{\kappa
m}}{2}\omega^2A^2\cos\frac{ka}{2}\overset{长波极限}{\rightarrow}\frac{\sqrt{\kappa
m}}{2}\omega^2A^2\)
波的反射:若端点固定则有半波损失,若自由,则无半波损失。
连续介质中的波动
波动方程为 \[ m\frac{\partial^2u_n}{\partial t^2}-c^2\frac{\partial^2u_n}{\partial x^2}=0 \] 以声波为例,其波动方程为 \[ \frac{\partial^2 \tilde{\rho}}{\partial t^2}-(\frac{\partial p}{\partial \rho})_0\frac{\partial^2 \tilde{\rho}}{\partial x^2}=0 \]
多普勒效应
\[ \frac{\nu'}{\nu}=\frac{c+u}{c-v} \] 马赫锥半顶角 \[ \alpha=\arcsin\frac{c}{v} \]
万有引力
开普勒三定律
①椭圆定律:所有行星绕太阳的轨道都是椭圆,太阳在椭圆的一个焦点上。
②面积定律:行星和太阳的连线在相等的时间间隔内扫过的面积相等。
③调和定律:所有行星绕太阳一周的恒星时间(\(T\))的平方与它们轨道半长轴(\(a\))的立方成比例,即\(\frac{T^2}{a^3}=k\),\(k\)称为开普勒常数,对于同一个中心天体而言\(k\)是个常数。
开普勒问题
在有心平方反比力场中的运动问题称为开普勒问题。
三个守恒量:能量,角动量,拉普拉斯-龙格-楞次矢量。
三种轨道:椭圆(\(E<0\)),抛物线(\(E=0\)),双曲线(\(E>0\))。
球体引力场
均匀薄球壳对内部物体引力为0。
潮汐力
\[ 引潮力\left\{\begin{matrix} (f_潮)_x=\frac{2G\Delta mM_月}{r_月^3}R_{\oplus }\cos \theta \\ (f_潮)_y=\frac{2G\Delta mM_月}{r_月^3}R_{\oplus }\sin \theta \end{matrix}\right. \]
狭义相对论
两个基本假设
等效原理:任何惯性系的物理规律相同。
光速不变原理:任何惯性系中真空光速均为\(c\)。
其它
其它的不咋考不作讲解。