Re:从阶乘开始的解析延拓
前言
阶乘是个我们早已熟悉的概念。这篇文章就是要从阶乘开始讲我们重要的解析延拓。
正文
解析延拓
回想我们首次接触阶乘时对阶乘的定义\(n!=\prod_{i=1}^{n}i\)，但是高数中又出现了斯特林公式，显然这个初等定义是无法给出斯特林公式的，于是我们就想找出某个函数\(f(x)\)使得\(f(n)=n!\)，我们回想起了函数方程的知识，我们就可以抽象出如下的函数方程\(f(x)=xf(x-1),f(1)=1\)。显然，\(f(x)\)的定义域是正整数，但是我们如果将小数，负数甚至是复数代进去又会怎样呢。这种想法并不罕见，例如我们最开始学幂的时候指数只能是正整数，到后来我们一步步扩展到有理数，实数，乃至现在的复数。这也是一种延拓，因此，下面我们可以正式拿出解析延拓的定义 若\(f_1(x)\)在区域\(\sigma _1\)内解析，\(f_2(x)\)在区域\(\sigma _2\)内解析，\(\sigma_1\cap \sigma _2=\sigma_{12}\)非空，且在\(\sigma_{12}\)内\(f_1(x)=f_2(x)\),则称\(f_1(x)\)和\(f_2(x)\)互为解析延拓。 且这个解析延拓是唯一的，即如果\(f_2(z)\)和\(f_3(z)\)都是\(f_1(z)\)在区域\(\sigma_2\)中的解析延拓，则\(f_2(z)=f_3(z)\)。这个定理我们不证，但需要说明的是，解析延拓的唯一性定理是复变函数的特有性质，实变函数是不可能有这样的性质的。
\(\Gamma\)函数
上面提到阶乘所需要满足的函数方程，这个方程显然有无数解，因为我们总可以通过插值的方法将这些点用一段光滑曲线进行连接，好在我们足够幸运，生在了21世纪，欧拉给出了一个很好的关于这个方程的解，它具有一个简单的形式并且在右半平面是解析的。我们称其为\(\Gamma\)函数。定义为 \[
\Gamma(z)=\int_{0}^{\infty}e^{-t}t^{z-1}\mathrm{d}t
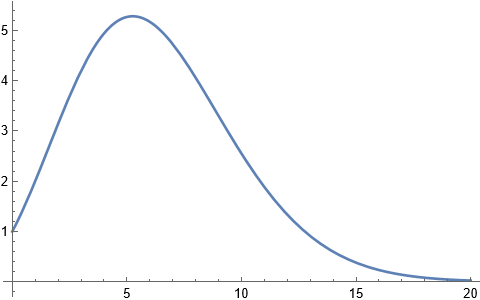
\] 它的收敛条件为\(Re(z)>0\)。我们可以画出当其宗量为实数时的图像
首先验证其是满足该函数方程的。 \[
\begin{aligned}
\Gamma(z+1)&=\int_{0}^{\infty}e^{-t}t^{z}\mathrm{d}t\\
&=-\int_{0}^{\infty}t^{z}\mathrm{d}e^{-t}\\
&=-(e^{-z}t^{z}|^{\infty}_0-\int_{0}^{\infty}e^{-z}\mathrm{d}t^{z}\mathrm{d}t)\\
&=-(e^{-z}t^{z}|^{\infty}_0-z\int_{0}^{\infty}e^{-z}t^{z-1}\mathrm{d}t)\\
&=-(0-z\Gamma(z))\\
&=z\Gamma(z)
\end{aligned}
\] 又易知\(\Gamma(2)=1\)，故\(\Gamma(n)=(n-1)!\)。 \(\Gamma\)函数还有一个重要性质。即\(\Gamma (z)\Gamma
(1-z)=\frac{\pi}{\sin(z\pi)}\)证明如下 \[
\begin{aligned}
\Gamma (z)\Gamma
(1-z)&=\int_{0}^{\infty}e^{-t}t^{z-1}\mathrm{d}t\int_{0}^{\infty}e^{-s}s^{-z}\mathrm{d}s\\
&=\iint_{0}^{\infty}e^{-(s+t)}(\frac{t}{s})^z\frac{1}{t}\mathrm{d}s\mathrm{d}t
\end{aligned}
\] 做变量代换 \[
\left\{\begin{matrix}
\zeta=s+t \\
\eta=\frac{t}{s}
\end{matrix}\right.
\] 则该变换的雅可比行列式为 \[
\begin{vmatrix}
\frac{\partial s}{\partial \zeta } & \frac{\partial s}{\partial
\eta } \\
\frac{\partial t}{\partial \zeta } &\frac{\partial t}{\partial
\eta }
\end{vmatrix}=
\begin{vmatrix}
(\frac{\partial \zeta}{\partial s })^{-1} & (\frac{\partial
\eta}{\partial s })^{-1} \\
(\frac{\partial \zeta}{\partial t })^{-1} &(\frac{\partial
\eta}{\partial t })^{-1}
\end{vmatrix}=\frac{\zeta}{(1+\eta)^2}
\] 则原积分变为 \[
\begin{aligned}
\iint_{0}^{\infty}e^{-(s+t)}(\frac{t}{s})^z\frac{1}{t}\mathrm{d}s\mathrm{d}t&=\iint_{0}^{\infty}e^{-\zeta}\eta^z\frac{1+\eta}{\zeta\eta}\frac{\zeta}{(1+\eta)^2}\mathrm{d}\zeta
\mathrm{d}\eta\\
&=\int_{0}^{\infty}e^{-\zeta}d\zeta\int_{0}^{\infty}\frac{\eta^{z-1}}{1+\eta}\mathrm{d}\eta\\
&=\int_{0}^{\infty}\frac{\eta^{z-1}}{1+\eta}\mathrm{d}\eta\\
&=\frac{\pi}{\sin(\pi z)}
\end{aligned}
\]
由该性质有\(\Gamma(\frac{1}{2})=\sqrt{\pi}\)。 \(\Gamma\)函数还有一个重要应用是计算形如\(\int_0^{\infty}x^ne^{-x^2}\)这样的积分。只需做一个简单换元，令\(t=r^2\)则原积分变为\(\int_{-\infty}^{\infty}r^{2x-1}e^{-r^2}dr\),即\(\Gamma(\frac{p+1}{2})=\int_{-\infty}^{\infty}r^{p}e^{-r^2}dr\)
\(B\)函数
定义 \[ B(p,q)=\int^{1}_{0}t^{p-1}(1-t)^{q-1}\mathrm{d}t \] 令\(t=\sin^2\phi\) \[ \begin{aligned} \int^{1}_{0}t^{p-1}(1-t)^{q-1}\mathrm{d}t&=2\int^{\frac{\pi}{2}}_{0}\sin^{2p-1}\phi \cos^{2q-1}\phi \mathrm{d}\phi \end{aligned} \] 容易发现\(B\)函数与\(\Gamma\)函数有如下关系 \[ B(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)} \] 证明如下 \[ \begin{aligned} \Gamma(p)=\int_{0}^{\infty}e^{-t}t^{p-1}\mathrm{d}t\\ \Gamma(q)=\int_{0}^{\infty}e^{-t}t^{q-1}\mathrm{d}t \end{aligned} \] 记上面两个式子中的t分别为\(x^2\)和\(y^2\)。 有 \[ \begin{aligned} \Gamma(p)=2\int_{0}^{\infty}e^{-x^2}x^{2p-1}\mathrm{d}x\\ \Gamma(q)=2\int_{0}^{\infty}e^{-y^2}y^{2q-1}\mathrm{d}y \end{aligned} \] 则 \[ \begin{aligned} \Gamma(p)\Gamma(q)&=4\iint_{0}^{\infty}e^{-(x^2+y^2)}x^{2p-1}y^{2q-1}\mathrm{d}x\mathrm{d}y\\ &=4\iint_{0}^{\infty}e^{-\rho ^2}(\rho \cos\theta)^{2p-1}(\rho \sin\theta)^{2q-1}\rho\mathrm{d}\rho \mathrm{d}\theta\\ &=2\int^{\frac{\pi}{2}}_{0}\sin^{2p-1}\theta \cos^{2q-1}\theta \mathrm{d}\theta\cdot 2\int_{0}^{\infty}e^{-\rho ^2}\rho^{2(p+q-1)}\mathrm{d}\frac{\rho^2}{2}\\ &=\Gamma(p+q)B(p,q) \end{aligned} \] 原式得证。 下面给出一个使用\(B\)函数的例子
超球体积
超球问题表述为，设\(N\)维空间中超球的方程为\(\Omega:\sum_{i=1}^{N}x_i^2\le
r^2\)。求该超球的体积。即求积分 \[
\int\cdots\int_\Omega dx_1\cdots dx_n
\] 为了解决这个问题，我们首先可以明确，\(N\)维超球的体积一定是如下形式 \[
V=V_nr^n
\] 其中\(V_n\)是单位超球的体积，即\(r=1\)时的超球体积。其次我们回想求三维空间球体积的时候，我们是将其切分为无数个二维的圆再进行积分操作。即先将\(x^2+y^2+z^2=1\)变成\(x^2+y^2=1-z^2\)再利用圆面积公式\(V=V_2 r^2\)求积分 \[
V_3=\int_{-1}^1V_2(1-z^2)\mathrm{d}z
\] 那么我们几乎可以同样这样来操作。即有 \[
\begin{aligned}
V_{n+1}&=\int_{-1}^{1}V_n(1-x_{n+1}^2)^{\frac{n}{2}}\mathrm{d}x_{n+1}\\
&=2V_n\int_{0}^{1}(1-x_{n+1}^2)^{\frac{n}{2}}\mathrm{d}x_{n+1}\\
&=V_n\int_{0}^{1}\frac{1}{x_{n+1}}(1-x_{n+1}^2)^{\frac{n}{2}}\mathrm{d}x_{n+1}^2\\
&=V_n\int_{0}^{1}t^{-\frac{1}{2}}(1-t)^{\frac{n}{2}}\mathrm{d}t\\
&=V_nB(\frac{1}{2},\frac{n}{2}+1)
\end{aligned}
\] 因此 \[\begin{aligned}
V_n&=V_{n-1}\frac{\Gamma(\frac{1}{2})\Gamma(\frac{n-1}{2}+1)}{\Gamma(\frac{n}{2}+1)}\\
&=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{n-1}{2}+1)}{\Gamma(\frac{n}{2}+1)}\frac{\Gamma(\frac{1}{2})\Gamma(\frac{n-2}{2}+1)}{\Gamma(\frac{n-1}{2}+1)}\cdots\frac{\Gamma(\frac{1}{2})\Gamma(2)}{\Gamma(\frac{5}{2})}V_2\\
&=\frac{\Gamma^{n-2}(\frac{1}{2})\Gamma(2)}{\Gamma(\frac{n}{2}+1)}V_2\\
&=\frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}
\end{aligned}
\] 故\(N\)维超球的体积公式为
\[
V=\frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}r^n
\] 