前言
笨人在自学理论力学的过程中感到数学基础不足,于是有了这篇文章。
前置知识只需多元函数微积分。ps:由于本人写作目的只是为了帮助学习
理论力学,因此本文所写知识的严谨性在数学上肯定欠佳,勿喷。
正文
来源
变分法的思想目前认为由雅各布伯努利在解决最速降线问题过程中提出。最速降线问题表述为:两端固定的光滑轨道,处于竖直向下的匀强重力场中,一个可视为质点的小球从顶端由静止开始滑落,问所需时间最小的轨道方程。
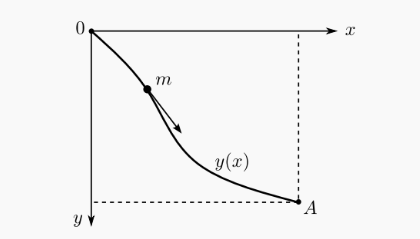 最速降线
最速降线
不妨构建如图所示坐标系,记轨道方程为。小球在内走过的长度是,速度是,因此有
可以看出只与相关。但它并不是我们常规意义上的函数,函数是数集到数集上的映射,而此时,我们的操作对象成了一个函数,因此我们称其为泛函。形如
由于在理论力学中,系统的拉式量仅依赖于广义坐标与广义速度,因此,我们在本文中只会着重讨论
的情况。
欧拉-拉格朗日方程
回想我们研究函数极值的方法,是对做一个小变换,来观察函数值的变化。在泛函中我们也采取类似的方法,不过此时我们所变换的是函数(但只是将变换约束在方向),由此来观察泛函的变化。 两式相减则得 我们又知 注意我们符号的记法,我们约定所作用的是泛函,所作用的是变量,由于之前我们已经说过,变换是仅局限于方向的,因此。所以 易知取极值条件为。
前文已经提过,可视作在方向对进行变换,而微分是在方向变化,因此微分和变分可以交换顺序(这当然是不严谨的证明,但正如前言所说,我们只是为了学习理论力学,至于严谨性,就交给数学家吧(笑))。因此,我们有如下式子
因此积分符号中第二项可变为
我们注意到该式可类比分部积分法变为 代入原积分得 又因为起点和终点的,所以上式最后一项总贡献为0。 为了确保我们要求
这个式子就是变分法中最重要的公式,欧拉-拉格朗日方程。
特别的,对于不显含的情况即的情况,我们可以将方程再度化简,首先做变换,上式即变为
又因为 因为,所以
代入得
最速降线的解决
回到我们开头提到的最速降线问题,在这个问题中,其不显含,且由于为常数,为了方便计算不妨令其取值为1,代入上面方程有
化简得
可以验证该方程有参数方程解,,该曲线即方程解,我们又称其为摆线。
一些碎碎念
最速降线的问题其实是雅各布伯努利的弟弟约翰伯努利
提出来为了证明他比他哥哥强的,约翰的方法他自认为聪明无比,他将小球的运动轨迹类比为光在一块折射率随变化的大玻璃中的运动轨迹,利用折射定律直接列出微分方程求解,然而费马定理在当时并未得到证明,好笑的是,他哥哥在求解最速降线的过程中首先提出变分法思想,后来费马定理的证明恰恰利用了变分法,这算不算打脸呢(笑)。
我懒得重新画图了,因此最速降线的图是直接从高显老师理论力学讲义里直接截下来的,所以会糊,懒得改了(
